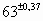|
Ressources : Cotes tolérancées , ajustement et jeu. |
Les cotes tolérancées.
L’impossibilité de réaliser une cote rigoureusement exacte par suite des imperfections des machines et des instruments de mesure, de l(usure des outils, oblige le constructeur à fixer les limites entre lesquelles la cote devra être réalisée. La distance entre ces limites est appelée « tolérance ».
Inscription des tolérances.
Tolérances chiffrées.
1) Inscrire après la cote nominale la valeur des écarts en plaçant toujours l’écart supérieur au-dessus.
2) Les écarts sont inscrits dans la même unité que la cote nominale ; c’est à dire en millimètre.
3) Ne pas mettre de signe lorsque l’écart est nul.
4) Lorsque la tolérance est répartie symétriquement par rapport à la cote nominale, ne donner qu’un écart précédé du signe ± ( plus ou moins).
Exemples :
ou
ou
Explications : Prenons l’exemple de la cote tolérancée
:
Cote nominale : CN = 32 mm
Écart supérieur : es = + 0,025 mm
Écart inférieur : ei = +0 ,009 mm
Cote maxi = CN + es = 32 + 0,025 = 32,025 mm
Cote mini = CN + ei = 32 + 0,009 = 32,009 mm
Intervalle de tolérance : IT = Cote maxi – Cote mini
= es - ei = 0,025 - 0,009
= 0,016 mm
Tolérances données par symbole ISO.
La cote nominale est suivie d’une lettre ( minuscule pou les arbres et Majuscule pour les alésages ) et d’un chiffre ; il faut consulter un tableau ( existant dans le GDI ) pour connaître les écart.
Exemples : 18 H 7 ou 36 h 6 ou 15 g 7
Les éléments du tolérancement.
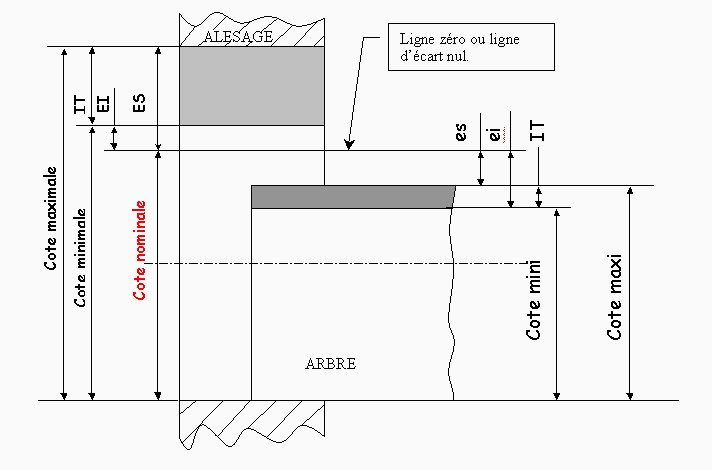
Les ajustements.
Un ajustement est constitué par l’assemblage de deux pièces de même dimension nominale. Il est désigné par cette dimension nominale suivie des symboles correspondant à chaque pièce, en commençant par l’alésage.
La position relative des tolérances détermine :
1) Soit un ajustement avec jeu [ Jeu > 0 ]
2) Soit un ajustement incertain, c’est à dire pouvant présenter tantôt un jeu, tantôt un serrage. [ JM> 0 et Jm< 0 ]
3) Soit un ajustement avec serrage. [ Jeu < 0 ]
Relations de calcul.
Jeu Max = Alésage Max – arbre min
Jeu min = Alésage min – arbre Max
IT Jeu = IT Alésage + IT arbre
( IT : Intervalle de Tolérance )
Exemples :
a) Alésage : f
arbre : f
JM=40,1 - 39,8 = 0,3 ( > 0 )
Jm=39,98 – 40,5 = -0,52 ( < 0 )
D’ou Ajustement Incertain.
b) Ajustement : f 32 H8f7 Alésage : f
arbre : f
JM=32,039–31,95=0,089(>0)
Jm = 32 – 31,975 =0,025(>0)
D’ou Ajustement avec jeu.