Sous l'action de charges répétées ou alternées, la rupture d'un matériau peut se produire sous des contraintes inférieures à la résistance du matériau en statique : c'est la rupture en fatigue. Cette rupture vient principalement de fissures microscopiques qui apparaissent dans le matériau dès les premiers cycles de chargement et qui progressent doucement à chaque fois que l'on sollicite le matériau. Il existe de nombreuses courbes pour définir la durée de vie en fatigue d'un matériau. Ces courbes sont issues de campagnes d'essais et reflètent le comportement statistique du matériau, elles sont souvent tracées à 95% de probabilité de résistance.
La courbe de Wohler
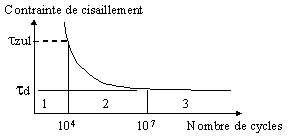
On trace sur la courbe de Wohler ou courbe S.N. (Stress-Number of cycles) l'amplitude de la contrainte de cisaillement alternée en fonction du nombre de cycles à la rupture. La contrainte moyenne est nulle.

Courbe de Wohler
On distingue trois zones sur la courbe de Wohler :
Le diagramme de Goodman
Pour un nombre de cycles donné N, on trace la courbe représentant la contrainte maximale acceptable avant rupture en fonction de la contrainte minimale.
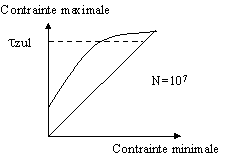
Diagramme de Goodman
Un point de fonctionnement est acceptable s'il reste en dessous de la courbe limite. La zone acceptable est toujours restreinte par la limite élastique en statique (en pointillés). Le diagramme étant en effet tracé en fonction de la rupture du matériau, la contrainte maximale est limitée à la contrainte statique maximale acceptable de manière à éviter une déformation du matériau dès les premiers cycles de fonctionnement.
Les diagrammes de Goodman des matériaux usuels sont fournis par la norme DIN pour 107 cycles (voir matériaux). En calculant la contrainte minimale et la contrainte maximale pour votre application, vous pouvez rapidement vérifier votre conception.
Le diagramme de Haigh
Avec le même principe que précédemment, on trace la courbe contrainte moyenne/contrainte alternée pour un nombre de cycles donné.
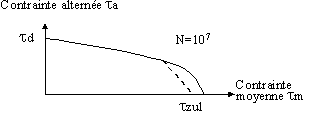
Diagramme de Haigh
On peut également vérifier que le fonctionnement retenu reste en dessous de la courbe limite.
Calcul du coefficient de sécurité en fatigue et données matériaux
Le diagramme de Haigh sert de référence pour calculer le coefficient de sécurité en fatigue en exploitant la représentation suivante :
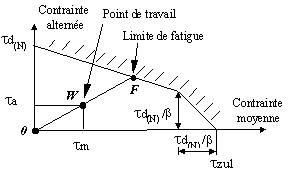
Représentation pratique du diagramme de Haigh
Le coefficient de sécurité en fatigue a F est le rapport OF/OW.
Il est déterminé de la manière suivante :
![]()
avec pour les ressorts de compression :
t m = 4 D R ( 2 L0 - L1 - L2 ) k / ( p d3 )
t a = 4 D R ( L1 - L2 ) k / ( p d3 )
Les données matériaux sont définies de la manière suivante :
Pour les ressorts de compression, la norme DIN fournit les diagrammes de Goodman pour les aciers et les inox courants (grenaillés et non grenaillés) pour 107 cycles (voir page matériaux).
Voici comment passer d'un diagramme de Goodman au diagramme de Haigh correspondant :
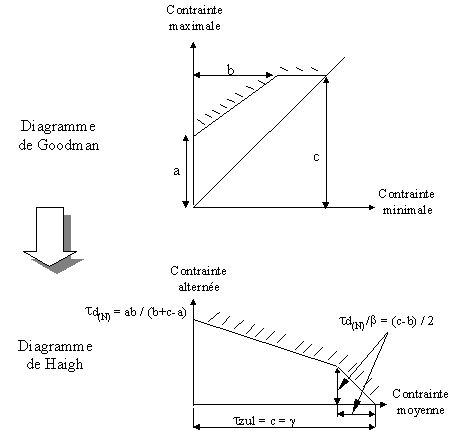
Les valeurs de a, b et c sont lues sur les diagrammes de Goodman pour 107 cycles. La formulation de t d(d), b et g peut ensuite être déterminée pour les matériaux utilisés.
Voici les formules et graphiques obtenus pour les aciers et inox usuels
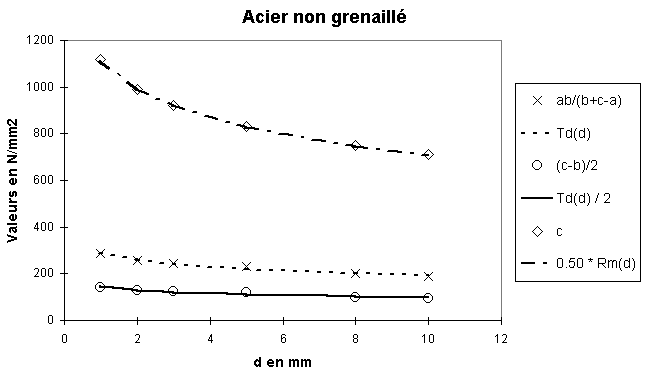
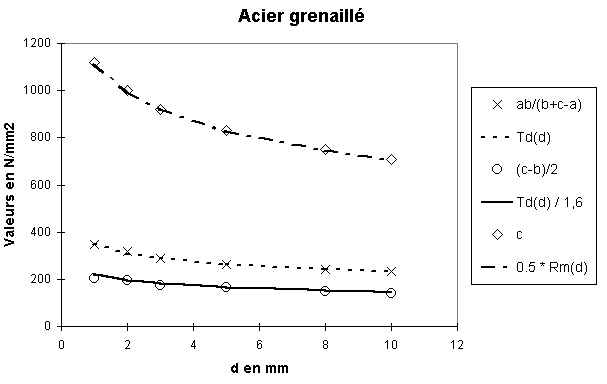
Données de fatigue pour l'acier DH (1 £ d £ 10 mm)
|
non grenaillé |
grenaillé |
||
|
b |
Sans unité |
2 |
1.6 |
|
t d |
N/mm2 |
293.5 / d0.1786 |
350.8 / d0.1769 |
|
t zul |
N/mm2 |
0.50 (2230- 355.94 Ln(d) ) |
|
|
t d(N³ 104) |
N/mm2 |
t d |
|
|
t d(104<N<107) |
N/mm2 |
|
|
|
t d(N£ 104) |
N/mm2 |
t zul |
|
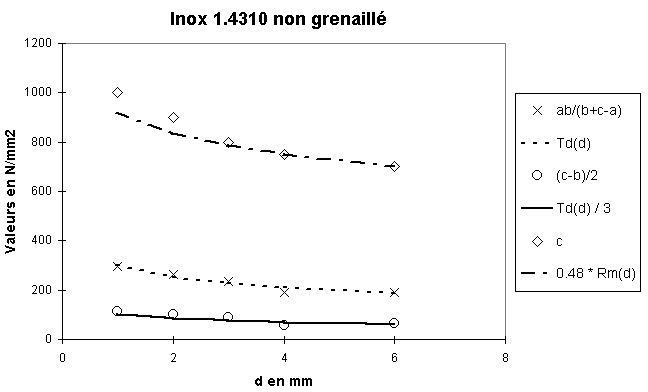
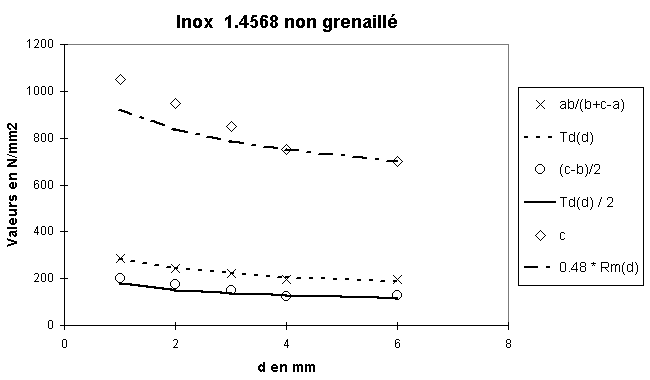
Données de fatigue pour l'inox (1 £ d £ 6 mm)
|
1.4310 non grenaillé |
1.4568 non grenaillé |
||
|
b |
Sans unité |
3 |
2 |
|
t d |
N/mm2 |
303 / d0.268 |
285 / d0.234 |
|
t zul |
N/mm2 |
0.48 (1918- 255.86 Ln(d) ) |
|
|
t d(N³ 104) |
N/mm2 |
t d |
|
|
t d(104<N<107) |
N/mm2 |
|
|
|
t d(N£ 104) |
N/mm2 |
t zul |
|