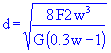
Méthode pratique de dimensionnement des ressorts de compression

L'objectif est de pouvoir dimensionner rapidement un ressort sans avoir de nombreux calculs à réaliser. La première partie du document résume les opérations à effectuer et donne des indications sur les valeurs qui doivent être renseignées. La deuxième partie montre pas à pas un exemple de calcul. La troisième partie présente en détail les diverses étapes de la méthode.

Première partie : méthode pratique

1ère étape : calcul de d mini théorique

Calculer :

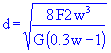
La valeur de d ainsi trouvée est la valeur minimale théorique.

2ème étape : choix de d réel et calcul de De

Pour déterminer le d réel, prendre la valeur supérieure acceptable la plus proche chez le fournisseur de fil.

Voici par exemple les diamètres de fils usuels fabriqués par AMIC (en mm) :

0.20

0.85

2.2

6.0

0.25

0.90

2.5

6.5

0.30

0.95

2.8

7.0

0.35

1.0

3.0

7.5

0.40

1.1

3.5

8.0

0.45

1.2

3.8

8.5

0.50

1.3

4.0

9.0

0.55

1.4

4.2

10.0

0.60

1.5

4.5

11.0

0.65

1.6

4.8

12.0

0.70

1.8

5.0

 

0.80

2

5.5

 

Un fois que d est choisi, calculer le diamètre extérieur du ressort : De = ( w + 1 ) d

et le diamètre moyen : D = w * d

 

3ème étape : calcul de nt et L0

Pour le calcul de L0, il faut fixer le type l'extrémité du ressort : ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

Les derniers calculs peuvent être définis selon plusieurs options.

Option 1 : la raideur R est imposée :

n = G d4 / ( 8 R D3 ) : nombre de spires utiles

L0 = n ( 0.3 D + 0.15 d ) + ni d

Option 2 : la longueur L0 est imposée :

n = ( L0 – ni d ) / ( 0.3 D - 0.15 d )

R = G d4 / ( 8 n D3 ) : raideur totale du ressort

Option 3 : la déformée totale f ( f = L0 – L2 ) est imposée :

n = f G d4 / ( 8 F2 D3 ) .

L0 = n ( 0.3 D + 0.15 d ) + ni d

Option 4 : rien n'est imposé :

n = 2 : ressort le plus court possible. En effet, selon les normes de calcul, n doit toujours rester supérieur à 2.

L0 = n ( 0.3 D + 0.15 d ) + ni d

Fin des options.

Pour trouver le nombre total de spires, faire nt = n + 2 pour les extrémités rapprochées (meulées ou non).

 

4ème étape : fin des calculs

Ca y est, le ressort est défini : De, d, nt, L0 sont connus.

Note : Vous pouvez jouer sur la valeur de w que vous avez fixée à la première étape pour trouver plusieurs solutions pour votre conception.

Un outil en ligne est à votre disposition (voir menu) pour effectuer des vérifications complètes et éventuellement ajuster la conception.

Deuxière partie : exemple

Calculer :

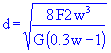
Pour notre problème : Le calcul donne d = 5.345 mm.
On choisit pour la suite d = 5.5 mm . C'est la première valeur supérieure acceptable dans le tableau (ci-dessus).

Diamètre extérieur du ressort : De = 5.5 * ( 10 + 1) = 60.5 mm.

Diamètre moyen : D = 10 * 5.5 = 55 mm.

Nous choisissons un ressort avec les extrémités rapprochées et meulées donc ni = 1.5

L'option de calcul est la suivante : la raideur est fixée à 5 N/mm.

On obtient ainsi
n = 70000 * 5.54 / ( 8 * 5 * 553 ) = 9.625 spires
L0 = 9.625 ( 0.3 * 55 + 0.15 * 5.5 ) + 1.5 * 5.5 = 175.00 mm.

nt = 9.625 + 2 = 11.625 spires.

Voila, le ressort est connu :
De = 60.5 mm ; d = 5.5 mm ; L0 = 175 mm ; nt = 11.625 spires.

Troisième partie : détail de la méthode

Le principe est de dimensionner le ressort à partir de la force maximale F qu'il doit supporter.

F2 est donc la donnée principale de calcul.

On conçoit un ressort à spires serrées pour tenir compte des hypothèses de calcul et des contraintes. D'une manière classique, le pas vaut 0.3 fois le diamètre moyen ( m = 0.3 D).

Pour une spire d'un tel ressort la déformation maximale vaut : delta = m - d = 0.3 D - d

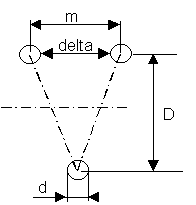
On souhaite au départ que la force F2 amène la déformation maximale soit :

F2 = R' * delta

R' est la raideur d'une spire donnée par l'équation : R' = G d4 / ( 8 D3 )

On obtient ainsi la relation : F2 = G d4 ( 0.3 D - d) / (8 D3)

On peut remplacer D par w * d ( w est le rapport d'enroulement du ressort). On obtient ainsi la relation suivante :

F2 = G d4 ( 0.3 w - 1) / (8 w3)

En fixant w (pour un ressort classique : w = 10) et G (matériau), il est alors possible de déterminer d :

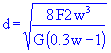
La valeur trouvée permet de choisir le d réel appliqué en prenant le diamètre de fil acceptable le plus proche qui reste supérieur à la valeur indiquée.

d est maintenant fixé.

Le diamètre extérieur du ressort est calculé : De = ( w + 1 ) d

Le ressort est initialement calculé pour arriver à spires jointives sous l'effort F2. Cependant, sous F2, le ressort finalement fabriqué doit respecter un espace minimal entre les spires. Cet espace est pris égal à 0.15 d (norme simplifiée). Le pas du ressort est ainsi modifié et prend la valeur m = delta + 1.15 d
Les expressions faisant intervenir L0 tiennent compte de cette considération.

La suite des opérations dépend du problème traité.

1 : Si la raideur R est imposée :

Le nombre de spires utiles du ressort est calculé :

n = R' / R.

Maintenant, la longueur libre du ressort peut être définie en respectant l'espace minimal entre les spires au cours du fonctionnement :

L0 = n ( delta + 1.15 d ) + ni d

Avec ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

2 : Si la longueur L0 est imposée :

Le nombre de spires utiles du ressort est calculé :

n = ( L0 – ni d ) / ( delta + 1.15 d )

Avec ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

La raideur totale du ressort obtenu est

R = G d4 / ( 8 n D3 )

3 : Si la déformée totale f ( f = L0 – L2 ) est imposée :

Le nombre de spires utiles du ressort est calculé :

n = f R' / F2.

Maintenant, la longueur libre du ressort peut être définie en respectant l'espace minimal entre les spires au cours du fonctionnement :

L0 = n ( delta + 1.15 d ) + ni d

Avec ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

4 : Si rien n'est imposé :

Prendre le ressort le plus court possible : n = 2 . En effet, selon les normes de calcul, n doit toujours rester supérieur à 2.

Maintenant, la longueur libre du ressort peut être définie en respectant l'espace minimal entre les spires au cours du fonctionnement :

L0 = n ( delta + 1.15 d ) + ni d

Avec ni = 1.5 pour les extrémités rapprochées et meulées et ni = 3 pour les extrémités rapprochées.

 

Pour trouver le nombre total de spires, faire nt = n + 2 pour les extrémités rapprochées (meulées ou non).

Ca y est, le ressort est défini : De, d, nt, L0 sont connus.