Lors de l'utilisation du ressort, il n'y a pas que le corps du ressort qui travaille, les branches ont aussi tendance à se déformer. Pour calculer correctement la raideur totale d'un ressort de torsion, il faut donc prendre en compte la flexion des branches.
La norme DIN indique comment calculer le supplément d'angle en degrés relatif à une branche non serrée (la sollicitation externe est transmise par un seul point de contact) avec un rayon d'appuis Ra :
pour une branche radiale non serrée
pour une branche tangente non serrée
Cela permet de calculer la raideur totale d'un ressort de torsion :
Avec Sa et Sb qui dépendent du type de branche utilisé :
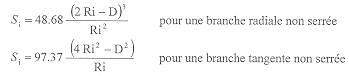
Nous obtenons ainsi la raideur totale d'un ressort à branches tangentes non serrées :
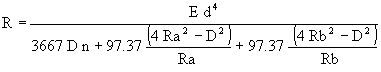
Cette formule dépend non seulement du type d'extrémités utilisé mais aussi des rayons d'appuis Ra et Rb. Contrairement aux ressorts de compression et de traction, la raideur totale n'est pas une caractéristique propre du ressort de torsion. Cette raideur dépend du fonctionnement associé au ressort.
Il faut noter que les formules de calcul de la déformation des branches sont approchées, elles entraînent une légère surévaluation de la raideur du ressort pour les déformations importantes. Dans la pratique certains constructeurs sont amenés à utiliser des coefficients correcteurs empiriques pour améliorer la précision des calculs. Nous n'avons pas trouvé de formules de calcul plus précises dans la littérature.